La capabilité d’un processus est définie comme étant l’aptitude ou la capacité de ce processus à satisfaire les spécifications du client.
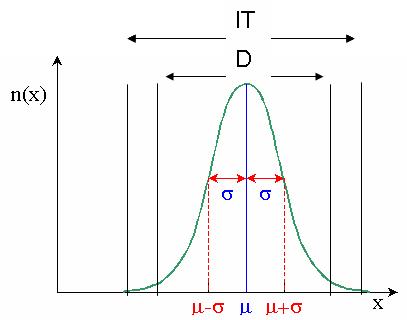
La capabilité se calcule pour une caractéristique d’un procédé qui suit une loi normale. La loi normale est une loi de distribution continue définie par deux paramètres : la moyenne et l’écart-type. Elle produit une courbe de Gauss qui répartit les valeurs des mesures de part et d’autre de la moyenne, de façon centrée. L’une des propriétés de la loi normale est de contenir 99,73% des mesures dans l’intervalle: µ-3σ ≤ x ≤ µ+3σ
•µ = m : moyenne
Dans le cas d’une loi normale, la moyenne est confondue avec la médiane et le mode
•IT : intervalle de tolérance, il correspond à la spécification client
•D : Dispersion, il s’agit de l’intervalle contenant 99,73% des produits soit 3σ
•σ : écart type
l’écart type se calcul grâce à la formule :
•m = moyenne
•N : Nombre de mesures
•Xi : valeurs
La capabilité, Cp, fait état de la capacité d’un processus à répondre aux spécifications du client. Elle compare la largeur de la plage de spécification (IT) à la dispersion des mesures.
Elle peut être estimée, de façon globale par la relation :
C = IT / D
Soit
C = IT / (6 σ)
Il existe deux types de capabilités: la capabilité process (Cpk) et la capabilité machine (Cpm)
LA CAPABILITE PROCESS Cpk
Cette capabilité mesure le centrage de la distribution par rapport aux limites de spécifications. Sa formule est la suivante :
•LTS : limite supérieure de spécification
•LTI : limite inférieure de spécification
LTS-LTI = IT
LTS et LTI sont les limites de la plage de spécification
En pratique, il faut:
Cp > 1,67
Cpk > 1,67
Cela permet une dispersion et un centrage satisfaisants. De plus Cpk doit avoir une valeur inférieure à celle de Cp. En cas de mauvais résultats deux cas sont possibles :
•Le Cp n’est pas bon, dans ce cas il y a un problème de répétabilité, il existe une grande variabilité entre deux mesures. Il faut alors se pencher sur la maîtrise du procédé et l’améliorer
•Le Cpk n’est pas bon, dans ce cas il s’agit d’un décentrage de la distribution par rapport à la moyenne. Un simple réglage suffira à recentrer la distribution
LA CAPABILITE MACHINE Cpm
Cet indicateur tient à la fois compte de la dispersion et du centrage. Il renforce l’analyse donné par le Cp et le Cpk. Il assure que la variabilité sur le produit est faible, que le procédé est bien centré sur la cible et donc que le taux de pertes reste acceptable. La capabilité machine ne peut être calculée que sur des pièces fabriquées sur la ou les mêmes équipements et pour les mêmes réglages.
Soit
Pour garantir une bonne capabilité machine, on doit avoir Cpm > 1,33
Important : le calcul des capabilité ne peut se faire que pour un procédé stable. Cette stabilité est obtenue par des méthode tel que le calcul de la reproductibilité et de la répétitivité (méthode R&R).
Copyright : INFOQUALITE
Partager cet article


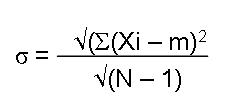
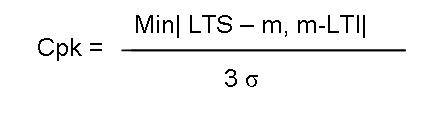
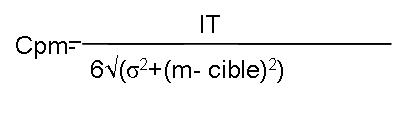
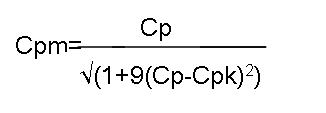
1 Comment
Comments are closed.